Transformation refers to the replacement of a variable by some function. In the logistic regression technique, variable transformation is done to improve the fit of the model on the data. Some of the common variable transformation functions are Natural Log, Square, Square-root, Exponential, Scaling (Standardization and Normalization), and Binning/ Bucketing. In this blog, we will take a practical example to understand the importance of variable transformation.
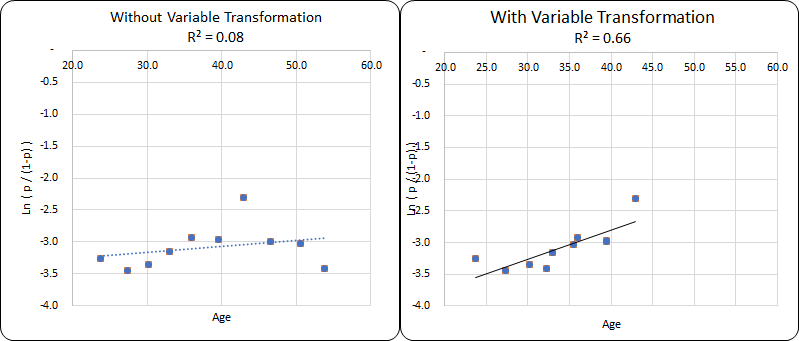
The featured image above shows the R-Squared value for the Age variable with and without transformation. The Age variable does not have a linear relationship with the log-odds and the R-Squared value is just 0.08. However, with transformation, we can fit the trend to be more linear and thereby increase the R-Squared to 0.66.
Logistic Regression with Age variable
import statsmodels.formula.api as sm import statsmodels.api as sma mylogit = sm.glm( formula = "Target ~ Age", data = dev, family = sma.families.Binomial() ).fit() mylogit.summary()
| Dep. Variable: | Target | No. Observations: | 10000 |
|---|---|---|---|
| Model: | GLM | Df Residuals: | 9998 |
| Model Family: | Binomial | Df Model: | 1 |
| Link Function: | logit | Scale: | 1.0000 |
| Method: | IRLS | Log-Likelihood: | -1863.2 |
| Date: | Fri, 03 Jul 2020 | Deviance: | 3726.5 |
| Time: | 15:23:56 | Pearson chi2: | 9.99e+03 |
| No. Iterations: | 6 | ||
| Covariance Type: | nonrobust |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -3.4545 | 0.200 | -17.261 | 0.000 | -3.847 | -3.062 |
| Age | 0.0109 | 0.005 | 2.199 | 0.028 | 0.001 | 0.021 |
The p-value of the Age variable is 0.028. Assuming you have set the alpha value as 0.01 for variable selection in your model then, the Age variable may be considered as not significant. As such, we will have to drop the age variable from the model.
Visualization Chart of Age Variable
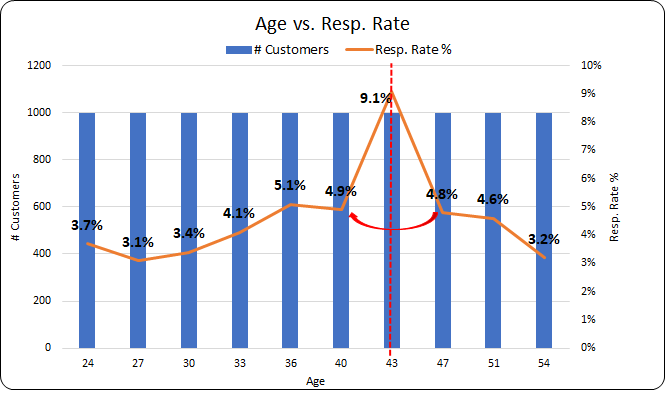
The visualization chart of Age shows that the response rate decreases after 43. We can probably make the age variable significant by some transformation function. Possible transformation functions are:
- Binning – Converting the Age variable from continuous to categorical
- Mirroring – Assume the Red-colored line as shown in the image to be a mirror and transform the values above 43 to reflect on the lower side.
Variable Transformation of Age in Python
The python code and the output below shows that the Age variable which was statistically insignificant can be made significant by the variable transformation.
## Variable Transformation of Age Variable ## DV is used for Derived Variable dev["DV_Age"]=dev["Age"].map(lambda x: 43-(x-43) if x>43 else x)
## Logistic Regression on Transformed Age Variable mylogit = sm.glm( formula = "Target ~ DV_Age", data = dev, family = sma.families.Binomial() ).fit() mylogit.summary()
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | -5.0110 | 0.325 | -15.411 | 0.000 | -5.648 | -4.374 |
| DV_Age | 0.0571 | 0.009 | 6.287 | 0.000 | 0.039 | 0.075 |
Practice Exercise
- Apply the binning approach of variable transformation on the Age variable, i.e convert Age variable from continuous to categorical
Final Note
Variable transformation is a very legal step and well-accepted industry practice. Some of the common reasons why we use transformations are:
- Scale the variable
- Convert non-linear relationship to linear relationship
- Reduce skewness
- To fit the best model on the given data
In the upcoming blog, we will learn about the Weight of Evidence concept to transform a categorical variable into a numerical variable.
<<< previous blog | next blog >>>
Logistic Regression blog series home

Recent Comments