Answers to Practice Exercises
In this blog, we provide answers to the practice exercises given in our blogs on Measures of Central Tendency – Mean, Median, Mode
Mean – Practice Exercise 1
A customer has taken three loans from the bank and the tenure of each loan is 5 years
- Personal Loan of Rs. 2 Lakhs at 14% rate of interest
- Car Loan of Rs. 8 Lakhs at 11% rate of interest
- Home Loan of Rs. 40 Lakhs at 9% rate of interest
What is the rate of interest for the overall Rs. 50 Lakh?
Answer
rate of interest = ( 200000 * 14% + 800000 * 11% + 4000000 * 9%) / 5000000
= (280001 + 88000 + 360000) / 5000000
= 476000 / 5000000
= 0.0952 (9.52%)
Mean – Practice Exercise 2
A small startup has 10 employees including the founders. The monthly salaries of all the employees is given in the table below:
| Emp. No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Monthly Salary (k) | 90 | 80 | 18 | 18 | 17 | 16 | 16 | 16 | 15 | 14 |
Find the mean salary?
Is mean salary the right measure? If not, then Why?
Which values in the above table are outliers? Should you trim the values from both ends? Compute the trimmed mean by removing only the outliers and not necessarily by trimming values from both ends.
Answers
Find the mean salary?
mean salary = (90+80+18+18+17+16+16+16+15+14) / 10 = (300/10)
mean salary = 30
Is mean salary the right measure?
No. Mean is impacted by outliers, the salary values 80 and 90 in the above data are outliers. As such we should compute trimmed mean.
Which values in the above table are outliers?
The values [90, 80] are outliers
Should you trim the values from both ends?
No. The extreme values are only on the higher side as such we need not trim on both the sides
Compute the trimmed mean:
We will compute the trimmed mean by trimming values on the higher extreme.
trimmed mean = (18 + 18 + 17 + 16 + 16 + 16 + 15 + 14) / 8
trimmed mean = 16.25
Median – Practice Exercise 1
Compute median from the below histogram.

Answer
Total Frequency (N) = 8 + 9 + 14 + 19 + 15 + 10 + 7 + 6 + 2
N = 90 (even number of observations)
The number of observations is even, as such, the median value will be an average of N/2 and (N/2 + 1) position values.
N/2 = 90/2 = 45
N/2 + 1 = 46
Let’s calculate the cumulative frequency
| Age | Frequency | Cum. Freq |
| 35 | 8 | 8 |
| 36 | 9 | 17 |
| 37 | 14 | 31 |
| 38 | 19 | 50 |
| 39 | 15 | 65 |
| 40 | 10 | 75 |
| 41 | 7 | 82 |
| 42 | 6 | 88 |
| 43 | 2 | 90 |
45th and 46th observation is 38
Median = (38 + 38) / 2
Median = 38
Median – Practice Exercise 2
A small startup has 10 employees including the founders. The monthly salaries of all the employees are given in the table below. Find the median salary.
| Emp. No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Monthly Salary (k) | 90 | 80 | 18 | 18 | 17 | 16 | 16 | 16 | 15 | 14 |
Answer
- The values are in descending order (No need to sort)
- N = 10 (Even)
- Median = (10/2 + ((10/2)+1)/2) / 2 => (5th observation + 6th observation)/2
- Median = (17 + 16) / 2 = 16.5
- Median = 16.5
Mode – Practice Exercise 1
Find the mode for the below histogram
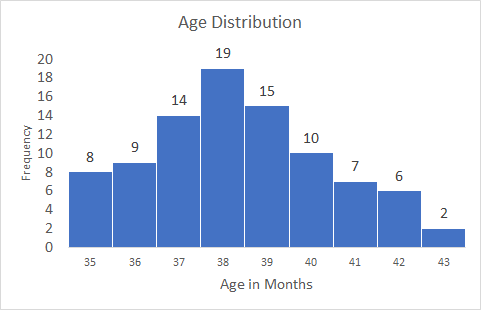
Answer
Mode Age = 38
Mode – Practice Exercise 2
A small startup has 10 employees including the founder members. The monthly salaries of all the employees is given in the table below. Find the mode salary.
| Emp. No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Monthly Salary (k) | 90 | 80 | 18 | 18 | 17 | 16 | 16 | 16 | 15 | 14 |
Answer
Mode Salary = 16
Next Blog
In the next blog, we will now discuss the measures of dispersion


Recent Comments