Training and Testing: Train – Test Split

The Training and Testing concept is an amazingly simple, time-tested approach. Right from our school days, we have been applying the Training & Testing approach to evaluate/grade the students. In schools & colleges, the teachers impart learning, knowledge, and skills to the students. How well the student has learned is then checked by tests (exams). Likewise, in Machine Learning, we first train the models and then test it.

Terminologies

Machine Learning: An algorithm that learns from data, identifies patterns in data, and store the learning in the form of a model.

Training Set: The dataset used for training/building the machine learning model is the Training Set.

Testing Set: The testing of the fitted model id done by checking its performance on unseen data called the Testing Set. The other term for Testing Set is Hold-out Sample.

Train – Test split

There are two approaches to splitting the population data for model development:

• Training and Testing set
• Development, Validation, and Hold-out

Training & Testing Set

You split the population into two sets – training and testing. The thumb rule is to randomly split the population dataset into training & testing having a 70:30 ratio. We build the model on the training set with cross-validation (explained later in this blog). Then we test the model on the testing set.

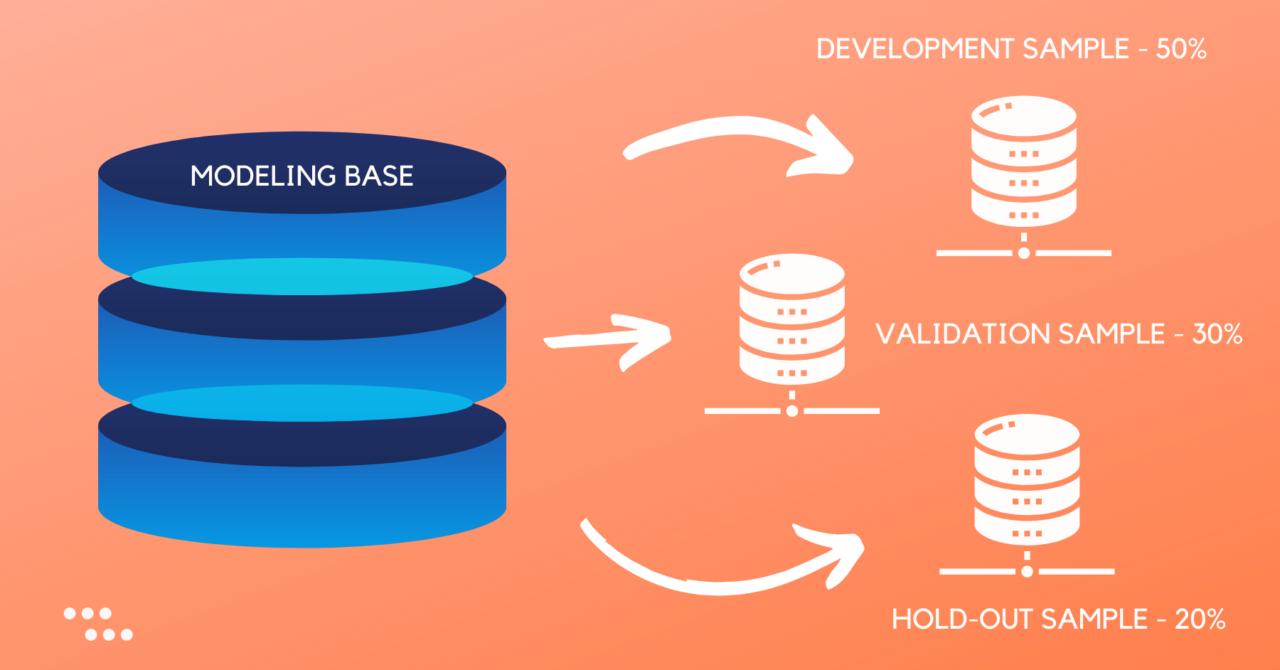
Development, Validation & Hold-out sample

In this approach, we split the population into three sets – Development, Validation, and Hold-out set.

• Development sample: The dataset used for training/developing the machine learning model is the Development Sample.
• Validation sample: The dataset used for testing and tuning the hyper-parameters of the model is the Validation Sample.
• Hold-out sample: A sample dataset kept aside in the very beginning of the model development to get an unbiased evaluation of the final model. The hold-out sample is not used (unseen) in the Model Development & Validation phase. The other term for the Hold-out sample is Testing Set.

Validation & Cross-Validation

Validation: We build the model on Development Sample. We validate the model on Validation Sample. Checking the performance of the development sample model on the testing (validation) data is Validation. As shown in CRISP-DM (Cross Industry Standard Process for for Data Mining), Model Development & Validation is an iterative process.

In the process, you iteratively build the model, test the model on validation data, and tweak the model based on model validation output. We stop the iterations when the desired model performance level is attained or no further improvement is possible.

Cross-Validation in machine learning is applied to get a reasonably precise estimate of the final model performance when applied to unseen data. Nowadays, most of the machine learning models are built using k-fold cross-validation. The value of k is generally set as 10.

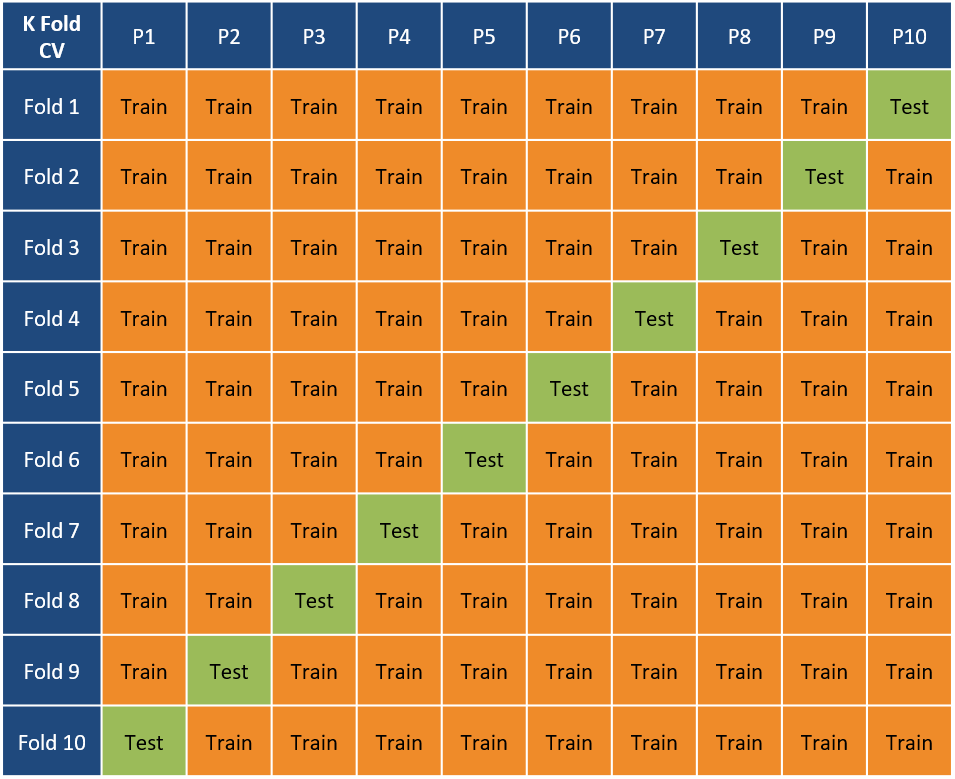
In Cross-Validation, the training data is split into K partitions. K-1 partitions are used as training data and the leftover 1 partition is considered as test data. As each fold proceeds the model built on k-1 partition is tested on the left-over partition. The final model performance is estimated as an average of the model performance on test partition in each fold.

Train – Test split code

Given below is the Python and R code to split a dataset into development, validation, and hold-out sample in 50:30:20 proportions.

# Python code to import the data 
import pandas as pd 
LR_DF = pd.read_csv("LR_DF.csv") 

LR_DF.shape (20000, 10)

# Code to split the data into development, validation and hold-out sample 

import numpy as np 
dev, val, holdout = np.split( 
     LR_DF.sample(frac=1, random_state=1212), 
     [int(.5*len(LR_DF)), 
     int(.8*len(LR_DF))] ) 

(len(dev), len(val), len(holdout))

# R code to import the data 
LR_DF <- read.csv("LR_DF.csv") 
dim(LR_DF) 

# Code to split the data into development, validation and hold-out sample 
set.seed(1212)
random <- runif(nrow(LR_DF), 0, 1) 
dev <- LR_DF[which(random <= 0.5),] 
val <- LR_DF[which(random > 0.5 & random <= 0.8 ),] 
holdout <- LR_DF[which(random > 0.8),] 
c(nrow(dev), nrow(val), nrow(holdout))

Sample Quality Check

In statistics, a sample refers to a set of observations (randomly) drawn from a population. A sample can have a sampling error. As such, it is desirable to do a quality check and ensure that the sample is representative of the population.

How can we find whether a sample is representative of the population?
We can find whether a sample is representative of the population by comparing the sample distribution with the population for a few important attributes. In our data, Target variable is the most important field. We will compare the target rate of the population with development, validation, and hold-out samples.

print("Population Response Rate :", 
      round(sum(LR_DF.Target)*100/len(LR_DF),2),"%" )

print("Development Sample Resp. Rate :", 
      round(sum(dev.Target)*100/len(dev),2),"%")

print("Validation Sample Resp. Rate :", 
      round(sum(val.Target)*100/len(val),2),"%")

print("Hold-out Sample Resp. Rate :", 
      round(sum(holdout.Target)*100/len(holdout),2),"%")

Population Response Rate : 4.44 %
Development Sample Resp. Rate : 4.6 %
Validation Sample Resp. Rate : 4.43 %
Hold-out Sample Resp. Rate : 4.05 %

cat("Population Response Rate :",
    round(sum(LR_DF$Target) * 100 / nrow(LR_DF),2), "%")

cat("Development Sample Resp. Rate :",
    round(sum(dev$Target) * 100 / nrow(dev),2), "%")

cat("Validation Sample Resp. Rate :",
    round(sum(val$Target) * 100 / nrow(val),2), "%")

cat("Hold-out Sample Resp. Rate :",
    round(sum(holdout$Target) * 100 / nrow(holdout),2), "%")

Population Response Rate : 4.44 %
Development Sample Resp. Rate : 4.39 %
Validation Sample Resp. Rate : 4.33 %
Hold-out Sample Resp. Rate : 4.73 %

Final Note

The concept of training – testing is extensively used by all data scientists when building any machine learning model.
Recommended Read: Wikipedia article – Training, validation, and test sets