Types of Variables
Knowingly / unknowingly, we all tend to use mathematics and numbers in our day-to-day life for decision-making. We can live with basic mathematics skills for our routine grocery shopping. However, if you are an aspiring data scientist then it is essential to have a very good understanding of statistical concepts. Even before we dive into statistics, one should have an understanding of the types of variables. So, let us begin our discussion on numbers by looking at them as variables (e.g. Age, Occupation, Income, etc) and variable types.
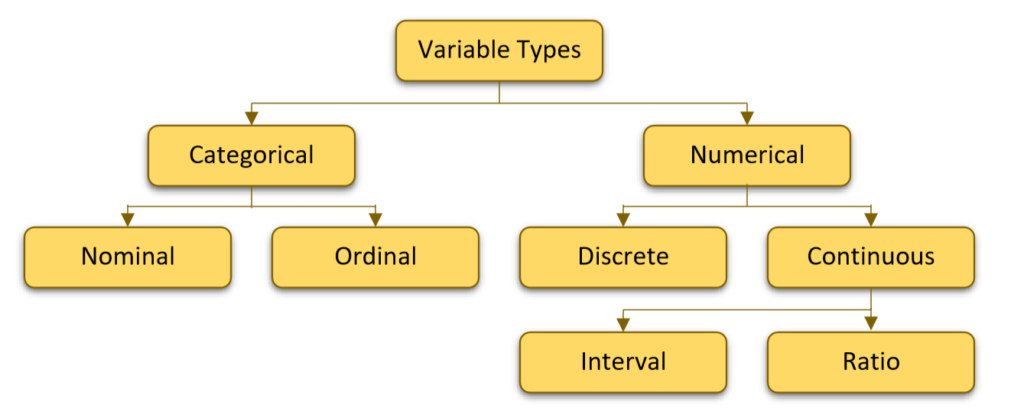
In Statistics, there are two types of variables. They are
-
- Categorical Variable
- Numerical Variable
Categorical Variable
- The Categorical variable is also known as a Qualitative variable. It represents the characteristics of the data object.
- Sometimes categorical variables take numerical values, but having numerical values doesn’t mean it has any mathematical meaning.
- There are two types of Categorical variables. They are
- Nominal Variables
- Ordinal Variables
| NOMINAL VARIABLE | ORDINAL VARIABLE |
|
|
Numerical Variable
- Numerical Variable is also called a Quantitative Variable.
- Numerical data is either an integer or a real value.
- It has a mathematical meaning.
- There are two types of Numerical Variables. They are,
- Discrete Variable
- Continuous Variable
Discrete Variable
- A Discrete Variable can only take certain distinct and separate values. But, it cannot take any intermediate value between them.
- Example: The number of transactions done by a customer on a particular day. It can 0, 1, 2, …. but it cannot be 2.5 or 2.75.
Continuous Variable
- A continuous variable can only take any continuous value.
- Example: Account Balance of the customer.
- There are two types of continuous variables. They are,
- Interval Variable
- Ratio Variable
| INTERVAL VARIABLE | RATIO VARIABLE |
|
|
Example:
| Nominal | Nominal | Nominal | Ordinal | Discrete | Interval | Ratio |
|---|---|---|---|---|---|---|
| Emp_ID | City | Department | Designation | No. of Subordinates | Months Since Last Leave | Salary |
| 2453 | Mumbai | Marketing | Vice President | 4 | 7 | 125000 |
| 2589 | Thane | Finance | General Manager | 7 | 6 | 80000 |
| 3048 | Surat | HR | Manager | 10 | 5 | 50000 |
| 2985 | Chennai | Operations | Asst. Manager | 5 | 4 | 30000 |
| 3184 | Delhi | Operations | Executive | 1 | 1 | 20000 |
| 1085 | Mumbai | Admin | Office Boy | 0 | 0 | 8000 |
Practice Exercise
Find the type of variables for the given deposit account data.
| Acc. No. | Acc. Type | Acc. Open Date | Length of Relationship (in Years) | Gender | No. of Txns. | Closing Balance |
| 1085100000065 | CA | 12-Jan-2020 | 0 | M | 5 | 79749.48 |
| 1085100000066 | CA | 1-Jan-2010 | 10 | F | 29 | 31905.80 |
| 1065100010065 | CA | 25-Jan-2015 | 5 | M | 15 | 339698.20 |
| 2085100000065 | SA | 10-Jan-2018 | 2 | M | 2 | 100.25 |
| 5000851000000 | SA | 15-Jan-2019 | 1 | F | 13 | 1000.00 |
Next Blog
In the next blog, we will discuss the measures of central tendency (Mean, Median, and Mode). The below table summarizes the best measure of central tendency for different types of variables.
| Type of Variable | Best Measure of Central Tendency |
| Nominal | Mode |
| Ordinal | situation-specific
(Mean, Median or Mode) |
| Interval/Ratio (not skewed) | Mean |
| Interval/Ratio (skewed) | Median |

Recent Comments